[정렬]05.병합 정렬

1. 기본 컨셉

 - 분할/정복(divide and conquer) 알고리즘에 기반한 정렬 방식

 - 요소들이 하나가 될 때까지 분할했다가  분할된 요소들을 크기에 따라서 정렬하는 방식

- 분할된 요소들이 그룹별로 정렬 된 후 다시 이전 요소와 비교해서 병합하는 방식

- https://www.youtube.com/watch?reload=9&v=XaqR3G_NVoo

 

2. 정렬 과정

 - 병합 정렬을 다음과 같이 재귀 함수 형태를 사용한다.

private void mergeSort(int[] arr, int si, int ei) {
	if (si < ei) {                   // 요소의 길이가 2개 이상일 때까지 계속해서 진행
		int mi = (si + ei) / 2;      // 중간 위치를 계산해서 배열 균등 분할 - Divide
		mergeSort(arr, si, mi);	     // 앞쪽 배열 정렬 - Conquer
		mergeSort(arr, mi + 1, ei);  // 뒤쪽 배열 정렬 - Conquer
		merge(arr, si, mi, ei);	     // 두 개의 list 병합 - Combine
	}
}

 

 - 배열의 시작 인덱스를 si, 끝 인덱스를 ei라고 정의한다.

 - si < ei일 때까지 중앙점 mi를 구하고 mi를 기준으로 나눈다. mi = (si + ei ) /2

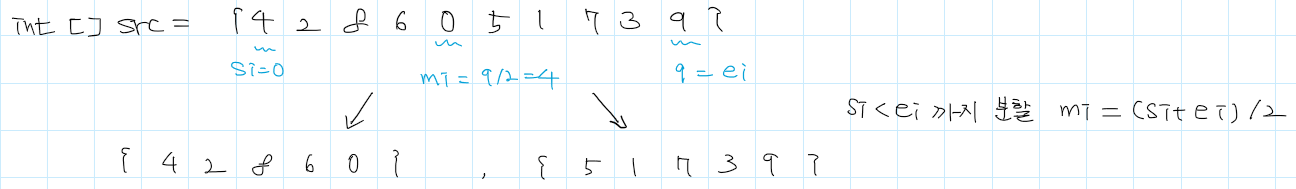
- 이 과정을 반복하다 보면 아래처럼 배열의 원소가 하나인 지점에서 재귀가 종료한다.

 - 이제 더 이상 쪼갤 수 있는 상태(si < ei)가 아니므로 각 요소들의 크기를 비교해서 병합한다.

 

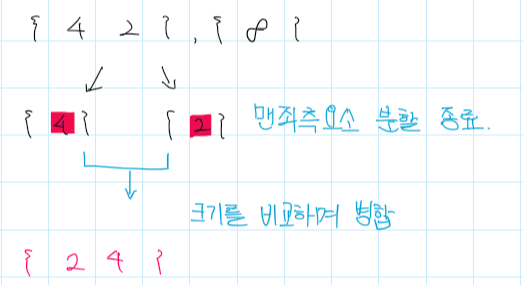
 - 다음으로 {8}도 이미 단일 원소로 구성되어있으므로 {2,4}의 원소들과 크기를 비교해서 병합한다.

 

 

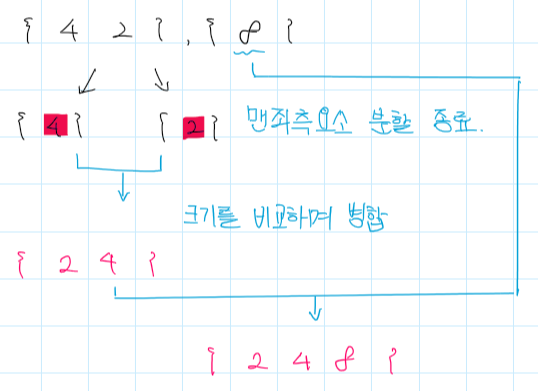
- {6,0}이 다시 분할 되서 {0}, {6} 이 되고 크기 비교 후 병합되어 {0, 6}이 되고 다시 {2, 4, 8) 과 합하게 된다.

 

- 오른쪽 부분도 유사한 과정을 거칠 것이고.

이제 왼쪽과 오른쪽 두 결과물이 합쳐지면.... 정렬이 완성된다.

 

 

3. 자바 코드

@Test
public void mergeSortTest() {
	mergeSort(data, 0, data.length-1);
}

private void mergeSort(int[] arr, int si, int ei) {
	if (si < ei) {// 요소의 길이가 2개 이상일 때까지 계속해서 진행
		int mi = (si + ei) / 2;// 중간 위치를 계산해서 배열 균등 분할 - Divide
		// 절반씩 mergeSort
		mergeSort(arr, si, mi);	//  앞쪽 배열 정렬 - Conquer
		mergeSort(arr, mi + 1, ei);	// 뒤쪽 배열 정렬 - Conquer
		merge(arr, si, mi, ei);	// 두 개의 list 병합 - Combine
	}
}

private void merge(int[] arr, int startI, int midI, int endI) {
	int i = startI;// 정렬된 왼쪽 배열에 대한 인덱스
	int j = midI + 1;// 정렬된 오른쪽 배열에 대한 인덱스

	int[] temp = new int[arr.length];// 정렬될 배열
	int k = startI;// 정렬될 배열에 대한 인덱스
		// 분할된 배열의 병합 처리 - 전반부와 후반부의 값들을 크기로 정렬
	while (i <= midI && j <= endI) {
		if (arr[i] <= arr[j]) {
			temp[k++] = arr[i++];
		} else {
			temp[k++] = arr[j++];
		}
	}
	// 아직 남은 부분이 있다면 배치
	while (i <= midI) {
		temp[k++] = arr[i++];
	}
	while (j <= endI) {
		temp[k++] = arr[j++];
	}
	// temp에 적힌 내용을 data에게 적용하기
	for(int t=startI; t<=endI; t++) {
		arr[t] = temp[t];
	}
}

1 - [2, 4, 8, 6, 0, 5, 1, 7, 3, 9]
2 - [2, 4, 8, 6, 0, 5, 1, 7, 3, 9]
3 - [2, 4, 8, 0, 6, 5, 1, 7, 3, 9]
4 - [0, 2, 4, 6, 8, 5, 1, 7, 3, 9]
5 - [0, 2, 4, 6, 8, 1, 5, 7, 3, 9]
6 - [0, 2, 4, 6, 8, 1, 5, 7, 3, 9]
7 - [0, 2, 4, 6, 8, 1, 5, 7, 3, 9]
8 - [0, 2, 4, 6, 8, 1, 3, 5, 7, 9]
9 - [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
정렬 완료: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

4. 정리

재귀가 본격적으로 사용되면서 앞서 살펴봤던 정렬들과는 비교할 수 없을 만큼 복잡해보이지만 시간 복잡도는 무려 O(nlogn)에 불과한 효율적인 정렬 알고리즘이다.